The Kaleidoscope Formula
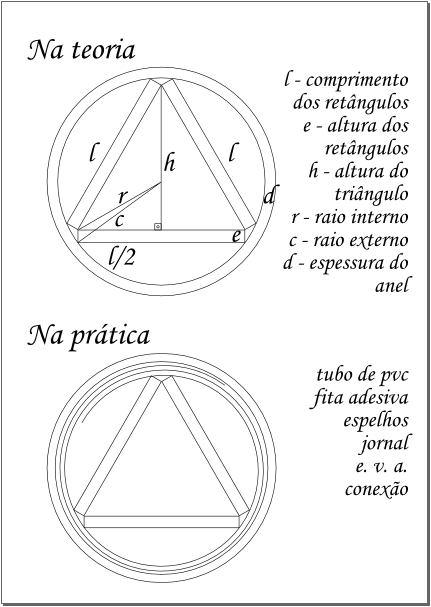
Esquema da visão do topo do Caleidoscópio, originalmente uploaded por mythus.A motivação
Em tempos imemoriais, passeando pelo Jardim Botânico, entrei com meus pais numa lojinha de conveniência. Minha mãe ficou brincando com um pedaço de pau que fazia o barulho a chuva; meu pai olhava o mapa, programando os lugares para ir; e eu fiquei admirado com um tubo de cartolina multicolorida com um buraco e, que me disseram depois, era um caleidoscópio. Lembro vivamente olhando para as árvores e para dentro da loja, maravilhado com os desenhos que se formavam. Não o compramos porque era muito caro, apesar de não fazer ideia de quanto custava ou mesmo ter noção de como é que meus pais conseguiam dinheiro. Não lembro de possuir um na infância ou de encontrar à venda caleidoscópios. Mas recordo deles em duas escolas que frequentei. Depois disso, só os encontrava no imaginário e na saudade infantil, até que depois de velho, ganhei um de presente.
Outro dia fui desafiado por uma garota de olhos de caleidoscópio a fazer um. Não faço ideia de quantas vezes usaram o desafio como psicologia negativa comigo. Quase sempre funciona quando se trata de algo que envolva a inteligência. Depois de séculos sem ver geometria, pus-me a riscar num guardanapo as fórmulas para gerar um caleidoscópio.
Dado um espelho, qual será o raio do tubo?
Numa visão de topo, o tubo é visto como anel; os espelhos como retângulos onde a largura é o comprimento e a espessura, sua altura. Tudo que lembro de geometria são apenas duas informações: Teorema de Pitágoras; e a regra de semelhança de triângulos.
1) Achei ![]() em função de
em função de ![]() , usando Pitágoras em
, usando Pitágoras em 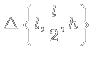 :
:
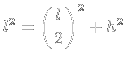
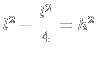
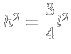
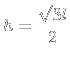 |
2) Achei
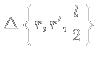 e
e 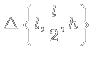 :
: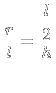
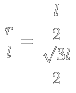
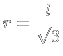
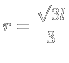 |
3) Chamei de
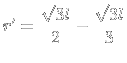
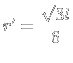 |
4) Achei
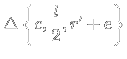 :
: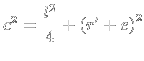
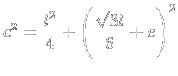
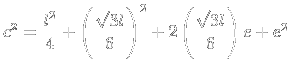
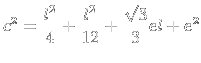
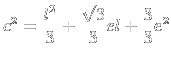
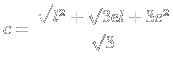 |
E o caminho contrário?
Eu só precisei de primeira parte, porque já tinha cortado os espelhos e precisava saber qual tubo e conexões seriam necessários. Dentre os que existem 25mm, 30mm, 40mm, 50mm, 60mm e por aí vai, quanto maior, mais caro. O detalhe é que essa medida é o diâmetro externo. Assim, é preciso considerar 5mm de espessura do tubo nos cálculos. E como o preço pode ser decisivo, pensei que talvez fosse bom considerar o diâmetro que se deseja ao caleidoscópio e, por ele, cortar os espelhos.
Voltando à última equação, isolei ![]() em função de
em função de ![]() e
e ![]() :
:
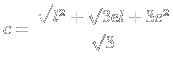
![]()
![]()
Lembram de 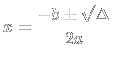 , onde
, onde ![]() ? Eu não lembrava, mas um amigo me relembrou (– Valeu, Andrei!).
? Eu não lembrava, mas um amigo me relembrou (– Valeu, Andrei!).
![]()
![]()
![]()
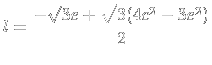
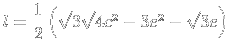 |
E na prática, funciona?
É bom ressaltar que os cálculos feitos são em função do raio. O diâmetro é o dobro do raio.
Um espelho normalmente tem 3mm de espessura. Os tubos de PVC têm entre 3 a 5mm de espessura, sem tanta precisão milimétrica, as medidas são dadas por seu diâmetro. Contudo, esse é o limite do universo milimétrico para as dimensões. Quando se vai cortar um espelho, pedir ao vidraceiro que corte uma medida em milímetros é certeza haver alguma variação: três centímetros e meio, pode até dar, mas 38mm vai ser difícil de fazer. Com um vidraceiro, trabalhe com centímetros.
Contando com a imprecisão do diâmetro interno do tudo de PVC, com a imprecisão do corte no espelho, com a imprecisão do artista que fixará os três espelhos formando o "triângulo equilátero" de espelhos (com as faces reflexivas voltadas para dentro, claro), é bom trabalhar com folgas. Elas também serão importantes para revestir os espelhos a fim de que não tenham contato direto com o tubo e fique amortecido contra choques e quedas. No meu caso, usei jornal: amassei bastante duas folhas de jornal para que o papel ficasse mole e grosso, depois estirei as folhas e envolvi com elas os espelhos. Para dar um acabamento, cortei meias luas de E. V. A.
A prova

Caleidoscopio, originalmente uploaded por mythus.O todo...

Caleidoscopio-visor, originalmente uploaded por mythus....é mais...

Caleidoscopio-espelhos, originalmente uploaded por mythus....que a soma...

VistaCaleidoscopica, originalmente uploaded por mythus....de cada uma...

ObjetosCaleidoscopicos, originalmente uploaded por mythus. ...de suas partes.
Sobre este post...
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html caleidoscopio.tex
Também foram usados: Kyle, Gedit, Inkscape e Gimp.
Uma versão em PDF pode ser baixada daqui.





0 comentários:
Postar um comentário